Bird's Eye View (BEV) Implementation: A Comprehensive Guide
Written by Purushothama Reddy Bandla 07 Mar, 2025
Bird's Eye View (BEV) is revolutionizing industries like autonomous driving, surveillance, and augmented reality, by providing a critical, top-down perspective that enhances spatial awareness and precision. As systems become more intelligent and autonomous, the ability to accurately interpret the environment from a BEV perspective is essential for safer navigation, real-time decision-making, and effective monitoring of complex scenarios.
Why is BEV so crucial today? The autonomous vehicles market is projected to reach a staggering $2.16 trillion by 2030, driven by advancements like BEV that enable enhanced navigation and safety. In surveillance, BEV aids in interpreting crowded scenes and tracking movements with heightened accuracy—a key capability within the smart surveillance market, which is expected to grow to $147 billion by 2030. Likewise, in augmented reality, BEV creates immersive experiences and precise spatial interactions, benefiting a sector poised to expand from $37 billion in 2023 to $114.5 billion by 2027.
In this blog, we will dive into the mechanics of BEV, from technical implementation to the critical applications driving its adoption. We’ll also walk through diagrams that clarify each stage, providing a clearer picture of how BEV empowers systems to better interpret and navigate their environments. Join us as we explore why BEV technology is shaping the future across multiple domains and what it means for innovation in today’s tech landscape.
1. Introduction to Bird's Eye View
What is Bird's Eye View (BEV)?
A Bird's Eye View provides a top-down representation of a 3D scene, offering a unique perspective that enhances spatial awareness – a key requirement in areas like autonomous vehicle navigation, robot path planning, and camera-based security systems. This high-level vantage point allows systems to perceive object relationships, track movements, and assess environments more accurately.
In computer vision, BEV is achieved by transforming a camera's default angle (typically front-facing or side-facing view) into a simulated overhead view. This process involves advanced techniques such as homography, projective geometry, and matrix which work together to reorient and warp the image, effectively flattening the scene into a comprehensive, top-down view. The result is a powerful tool for machines to better understand and interact with complex spatial environments, enabling safer and more efficient automated operations.
Applications of Bird's Eye View
- Autonomous Driving: BEV technology is critical for self-driving cars, enabling them to interpret their surroundings, including the position of other vehicles, pedestrians, and road markings and obstacles. By providing a top-down view, BEV allows the vehicle’s AI to make more accurate and timely decisions, enhancing both safety and efficiency on the road.
- Surveillance Systems: In video surveillance, BEV helps monitor extensive areas by offering a comprehensive top-down view of the space. This perspective allows security personnel to track movements, detect anomalies, and cover more ground with fewer cameras, improving overall security while reducing blind spots. BEV in surveillance is especially beneficial in applications like smart city monitoring, airport security, and stadium event management, where clear situational awareness is paramount.
- Augmented Reality: In AR applications, BEV enhances user immersion by allowing viewers to interact with environments from an overhead perspective. This added spatial context is valuable in fields like architecture, gaming, and urban planning, where users benefit from an enhanced understanding of layout and spatial relations. BEV enables users to switch between perspectives, increasing both the realism and functionality of AR experiences, ultimately improving user engagement and understanding.
These diverse applications demonstrate BEV’s transformative impact across industries, making it a key component in advancing automation, security, and interactive technologies.
2. Core Concepts in Bird's Eye View Implementation
2.1 Camera Projection and Perspective Transformation
The primary challenge in generating a Bird's Eye View (BEV) is transforming an image captured from a specific 2D perspective into a top-down view, which involves complex mathematical operations known as projective transformations.
When a camera captures a scene, it creates a projection onto the image plane on its particular viewpoint. To transform this viewpoint into a Bird's Eye perspective, we apply a homography transformation- a process that maps points from one plane to another. Homography leverages the principles of projective geometry, enabling us to “warp” the captured image and recreate the scene as if viewed directly from above. This transformation is essential in BEV applications because it reconstructs spatial relationships in the scene, allowing systems to interpret depth, distance, and relative positioning with high accuracy. Through these transformations, BEV enhances machine perception, making it indispensable in fields like autonomous navigation, robotic path planning, and spatial analytics.
Homography and Matrix Representation
In computer vision, the homography matrix (H) plays a crucial role in projective transformations between two planes. This matrix enables the mapping of points from one plane (such as the camera’s natural perspective) to another plane (like a top-down, Bird's Eye View), providing an essential tool for perspective manipulation.
The homography transformation preserves straight lines, making it particularly valuable for applications like BEV in autonomous driving. By ensuring that roads, lane markings, and objects maintain their correct orientation and positioning from an overhead perspective, the homography matrix helps create a reliable and geometrically accurate view.
Mathematically, the homography matrix is a 3x3 matrix and is denoted as:
$$ H = \begin{bmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix} $$
This matrix defines the relationship between points in the source image (from the original camera view) and their corresponding points in the target image (the BEV)).
The transformation of a point P(x,y) in the source image to P′(x′,y′) in the target image is governed by the following equation:
$$ \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = H \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} $$
This equation maps the coordinates from the source image to the Bird's Eye View.
2.2 Calibration of Camera Parameters
Camera calibration is the process of estimating a camera’s intrinsic and extrinsic parameters to establish the relationship between 3D world coordinates and the 2D image coordinates captured by the camera.
When an image is captured, the camera projects the 3D scene onto a 2D plane, which can introduce distortions. To map points in the 2D image back to their accurate positions in the 3D world (or vice versa), it’s essential to understand how the camera projects and potentially distorts the image. Camera calibration allows us to correct for lens distortion and enables precise mapping of 3D points to their 2D projections, ensuring spatial accuracy and fidelity.
Intrinsic Parameters:
Intrinsic parameters describe the internal characteristics of a camera, defining the relationship between the camera's image plane and pixel coordinates. These parameters include:
- Focal Length: Defines how much the camera zooms in or out, controlling the scale of objects in the image. The focal length is typically represented in terms of the x and y axes: fx and fy.
- Principal Point: The pixel coordinates of the optical center of the camera, where the optical axis intersects the image plane. It is represented as (Cx, Cy).
- Skew Coefficient: The angle between the x and y axes, usually close to 90°. In most consumer cameras, this value is negligible, but for certain specialized lenses, this could affect the image.
- Distortion Coefficients: Most camera lenses cause some level of distortion, especially wide-angle lenses. This distortion can be of two types:
- Radial Distortion: Causes straight lines to appear curved (barrel or pincushion distortion).
- Tangential Distortion: Occurs when the lens and the image plane are not perfectly aligned.
These intrinsic parameters can be represented in a matrix, often referred to as the intrinsic matrix K:
$$ K = \begin{bmatrix} f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} $$
Where:
- fx and fy, are the focal lengths along the x and y axes.
- Cy and Cy, are the coordinates of the principal point.
- s is the skew coefficient (usually negligible).
Extrinsic Parameters:
Extrinsic parameters describe the camera's position and orientation relative to the world. They consist of:
- Rotation Matrix (R): Describes the camera's orientation in the world.
$$ R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{bmatrix} $$
- Translation Vector (T): Describes the camera's position in the world. The translation vector has three components representing the camera's displacement along the x, y, and z axes.
$$ T = \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix} $$
The extrinsic parameters essentially map the 3D world coordinates to the camera’s coordinate system.
3. Steps in Implementing Bird's Eye View
3.1: Calibration and Setup
Begin by calibrating the camera to obtain its intrinsic and extrinsic parameters. Typically, this is achieved using a chessboard calibration technique. The known geometry of the chessboard provides a reliable reference, allowing the system to compute the necessary camera parameters accurately.
3.2: Detecting Key Points for Homography
Next, identify key points (such as corners, edges, or road markings) in both the original camera view and the desired top-down BEV plane. Establishing correspondences between these points is crucial to compute the homography matrix that will transform the perspective.
3.3: Warping the Image Using Homography
With the homography matrix calculated, you can warp the original image into the Bird's Eye View by applying the matrix transformation to each pixel. Many computer vision libraries, such as OpenCV, provide functions to streamline warping operation. For instance, the 'warpPerspective' function in OpenCV enables this transformation:
Warp the image to Bird's Eye View using the homography matrix
bird_eye_view = cv2.warpPerspective(image, homography_matrix, output_size)
3.4: Post-Processing and Refinement
After warping the image, some post-processing may be necessary to address any distortions or artifacts caused by the transformation. Techniques such as edge detection, filtering, and contrast adjustment can enhance the clarity and quality of the final the final Bird's Eye View.
4.Advanced Considerations
4.1 Handling Multiple Camera Inputs
In complex systems, especially those in autonomous vehicles, multiple cameras are used to generate a 360-degree Bird's Eye View. These cameras capture overlapping fields of view requiring sophisticated stitching algorithms to seamlessly combine them into a single, coherent top-down image. This multi-camera approach expands the BEV's field of view, improving environmental awareness and navigation precision.
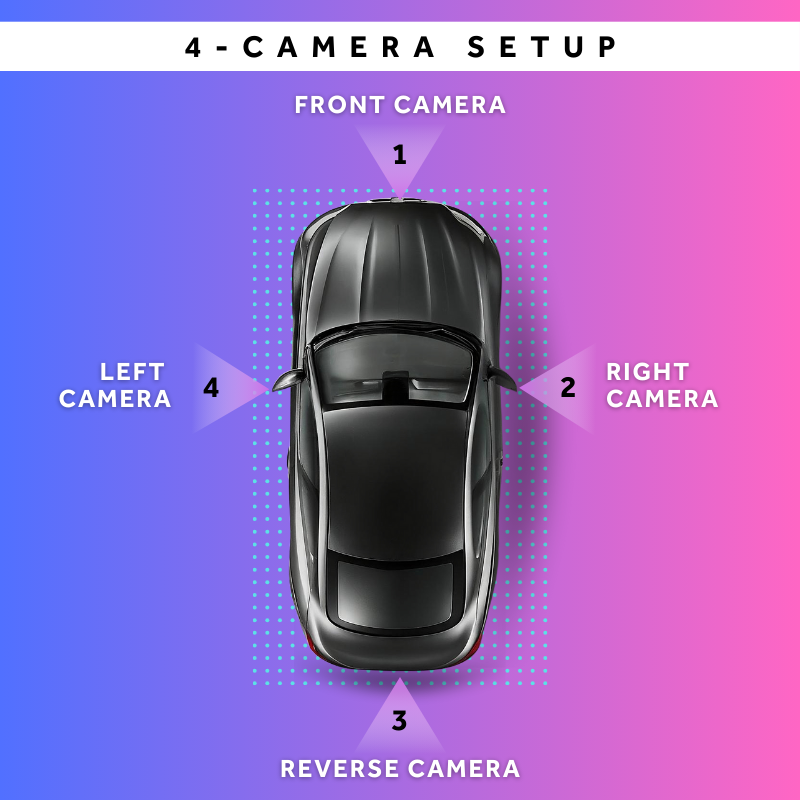
Multi-Camera Setup for 360° BEV
4.2 Object Detection in Bird's Eye View
Once generated, the Bird’s Eye View can serve as input for object detection algorithms allowing for the identification of vehicles, pedestrians, and obstacles from the top-down perspective. This approach enhances safety and reliability in applications like autonomous driving by providing a comprehensive view of the surrounding environment, making it easier to track and respond to potential hazards.
5. Conclusion
Bird's Eye View (BEV) is a transformative computer vision tool that converts scenes into top-down perspectives, enhancing spatial understanding and decision-making in applications such as autonomous driving, surveillance, and robotics. Implementing BEV involves critical steps, including camera calibration, homography computation, and image warping, to generate precise overhead views.
Advancements in multi-camera configurations and deep learning are continuously refining BEV technology, expanding its capabilities in spatial perception and real-time decision-making. Mastering BEV implementation empowers developers and engineers to build more intelligent, reliable vision-based systems across diverse fields.
At Cyient, we have developed a BEV framework tested with four top-mounted vehicle cameras. Our solution manages camera calibration, projection matrix generation, image projection for BEV, and image stitching to produce a seamless 360° surround view. To ensure accuracy, we have established a dedicated vehicle physical simulation lab for BEV framework testing and a camera calibration facility to fine-tune camera parameters.
About the Author

Purushothama Reddy Bandla
Technical Architect, Automotive Tech Practice
Purushothama is a software architect/developer and has pursued his master’s in VLSI Design. He has over 15 years of embedded and automotive industry experience with an interest in building new end-to-end AI solutions that accelerate human well-being and developing different autonomous models for human-friendly interactive machines in the automotive and agriculture fields.
.png?width=774&height=812&name=Master%20final%201%20(1).png)